Recently there has been a discussion of the so-called ?Fed Model,? with some questioning the validity of model, and others affirming it. Even the venerable John Hussman has commented on models akin to the Fed Model that he dislikes. This piece aims at taking a middle view of the debate, and explain where the Fed Model has validity, and where it does not.
What is the Fed Model?
The Fed Model is a reasonable but imperfect means of comparing the desirability of investing in stocks versus bonds. It can be considered a huge simplification of the dividend discount model, applied to the market as a whole, rather than an individual stock. The dividend discount model states that the value of the stock is equal to the future stream of dividends discounted at the corporation?s cost of equity capital.
What simplifying assumptions get applied to the dividend discount model to create the Fed Model?
- The market as a whole is considered rather than individual stocks.
- A constant ratio of earnings is paid out as dividends.
- The growth rate of earnings is made constant.
- A Treasury yield (or high/moderate quality corporate bond yield) is substituted for the cost of equity capital.
- Instead of following a strict discounting method, the equation is rearranged to make an explicit comparison between bond yields and equity yields.
Assuming that the dividend discount model is valid, or at least approximately so, what do these simplifying assumptions do to the accuracy of valuing the market as a whole? The first assumption is more procedural in nature, and does no major harm. The fifth assumption simply reorganizes the equation, and doesn?t affect the outcome, but only the presentation. The real changes come from assumptions 2-4.
Dividends are more stable than earnings, so the payout ratio certainly varies over time. Additionally, corporations have shown less willingness to pay dividends, and investors have shown less inclination to demand dividends, to the payout ratio today is roughly half of what it was in the early 60s.
Earnings don?t grow at a constant rate, either. Over the last 53 years, earnings have grown at a 6.7% rate, but that has included times of shrinkage, and boom times as well.
As for the cost of capital to a corporation, I believe that the Capital Asset Pricing Model is genuinely wrong, and I refer you to Roll?s famous critique for what should have been its burial. Academics need risk to be something simple though, with risk being the same for all investors (not true), so that they can easily calculate their models, and publish. The CAPM provides useful, if mistaken, simplification to financial economists. It is not going away anytime soon.
One day I will write an article to explain my cost of equity capital methods in more depth, which derive corporate bonds and option pricing theory. In basic, for any corporation, the basic idea is to compare the riskiness of the equity to that of a bond. Look at the yield on juniormost debt security of the firm, the cost of equity is higher than that. Examine the implied volatility [IV] on the longest dated at the money options for the firm. How do those implied volatilities compare with other firms? In general the higher the IV, the higher the cost of equity capital.
Practically, when looking at the capital structure of the firms in the S&P 500, I think that the yield on a BBB bond plus a spread could be a good proxy for the weighted average cost of capital for the firms as a group. I?ll get to what that spread might be in a bit. We have BBB yield series going back a long way. Equity risk for the S&P 500 (a high credit quality group) is probably akin to the risk of owning weak BB or strong single-B bonds on average. (My rule of thumb for cost of equity capital in an individual corporation is take the juniormost debt yield and add 3%. For those with access to RealMoney, I have written more on this here.)
To summarize then: there?s not much I can do about assumptions 2 and 3. The only thing I might say is that earnings are a better proxy for value creation than dividends, and that expectations for longer-term earnings growth do not change nearly as much as actual earnings growth does. On assumption 4, a BBB bond yield plus a spread will be a reasonable, though not perfectly accurate proxy for the cost of equity. My view is that spread should be between 2.5%-3.0%.
The Results
With that, the ?Fed Model? boils down to a comparison of BBB bond yields less a spread versus earnings yields. Wait, ?less? a spread? Didn?t I say ?plus? above?
Let?s consider how a stock differs from a bond. With a bond, all that you can hope to get is your principal and interest paid on a timely basis. With equity, particularly in a diversified portfolio, one can expect over the long term growth in the value of the business from a growing dividend stream, and reinvestment of retained earnings. As I mentioned above, that has averaged 6.7%/year earnings growth over the past 53 years.
If I were trying to balance the yield needed from bonds to compete with equities, it would look like this, then:
Earnings Yield + 6.7% = BBB bond yield plus 2.5-3.0%
Or,
Earnings Yield = BBB bond yield – 4% (or so)
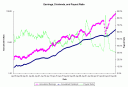
Here is how earnings yields and BBB bond yields have compared over the years.
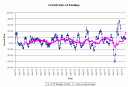
Thus my criteria for investing would be under the ?Fed Model,? when the earnings yield is more than 4% less than the BBB bond yield, invest in bonds. Otherwise, invest in stocks. Following this method, how would a portfolio have done since 1954?
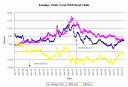
Wow. Pretty good rule, in hindsight. Is the spread of 4% the best spread for simulation purposes?
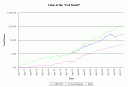
Pretty close. The optimum value is 3.9%. This chart uses an actuarial smoothing method to give a fairer view of noisy historical results. (Life actuaries use this smoothing method in cash flow testing to calculate required capital, because sometimes small changes in spread produce large differences in the results for a particular scenario.)
The strategy produces a return roughly 2.0%/year higher than investing in stocks only, with a standard deviation roughly 1.5%/year lower. At least in a backtest, my version of the ?Fed Model? works.
Limitations
Okay, given the above, I endorse my version of the ?Fed Model? as being useful, but with five caveats:
The first thing to remember is that the ?Fed Model? doesn?t tell you whether stocks are absolutely cheap, but whether they are cheap versus bonds. There may be other more desirable asset classes to choose from: cash, commodities, international bonds or equities, etc.
The second thing to remember is that when interest rates get low, yields do not reflect the true riskiness of bonds ? a slightly superior model would be 107% of BBB yields less 4.7%. But that could just be an artifact of backtesting. To its credit though, the slightly superior model behaves the way that it should in theory, in term of how credit spreads move.
Number three, ideally, all models would not use trailing earnings yields, but expected earnings yields. That said, trailing yields are objective, and expected yields have often proiven wrong at turning points.
The fourth limitation: a high earnings yield might reflect low earnings quality or profit margins higher than sustainable. No doubt that is possible, and particularly in the current era. On the flip side, there may be times when a low earnings yield might reflect high earnings quality or profit margins lower than sustainable. A rule is a rule, and a model is only a model; they don?t reflect all aspects of reality, they are just tools to guide us.
What P/E ratio would the current BBB bond yield (6.74%) support? I am surprised to say that it would support a P/E in the high 30s; 39.8 for the simple model, and 35.2 for the ?slightly superior? one. With the current trailing P/E at 18.1, that would indicate that on an unadjusted basis, the market could be twice as high as it is presently.
That thought makes me queasy, but here three other ways to look at it:
- How inflated are profit margins? If they are going to regress by less than half, then stocks are still a bargain.
- Are bond yields/spreads too low? The recycling of the current account deficit into US debt instruments keeps yields low, and the speculation in the credit markets keeps spreads low. What should be the normalized BBB yield?
- Will earnings growth slow beneath the 6.7% average? If so, the spread needs to come down.
Fifth, this is simply a backtest, albeit one that conforms to my theories. The future may not resemble the past.
Conclusion
My version of the Fed Model provides us with a way of comparing corporate bond yields with earnings yields, giving credit for growth that happens in capitalist economies that are free from war on their home soil. There are reasons to think that current profit margins are overstated, and perhaps that corporate bond yields will rise. All of that said, there is a large provision for adverse deviation in the present environment.
I would rather be a moderate bull on stocks versus bonds in this environment as a result. Don?t go hog wild, but current bond yields are no competition for stocks at present. If you think bond yields will normalize higher, perhaps cash is the place you would rather be for now.

Good article, but hard to read, because of some stray HTML code after every paragraph.
It looks like this:
Anybody else having difficulty viewing the post? If so, I’ll do some surgery on the HTML.
i’m having the same problem
The HTML should be fixed now… please tell me if you are still having problems…
This is a very interesting approach, and most helpful. As you know, I think that any method that includes both earnings and interest rates is vastly superior to one that does not. As you know, I prefer to use forward earnings and then consider the possible changes as sentiment.
The asset class that many individual investors have opted for is real estate.
You are quite correct in portraying the Fed model as a stocks versus bonds choice (with cash being a close equivalent these days). The gap reflects the widespread skepticism about future earnings, despite the multi-year pattern of companies beating expectations.
I’ll try to write something more careful and link to you, but meanwhile, any thoughtful investor should appreciate your careful analysis.
Jeff
Excellent piece David. I think one of your most important points is that “the ?Fed Model? doesn?t tell you whether stocks are absolutely cheap, but whether they are cheap versus bonds.” I agree and I have never thought of the Fed model as a pure buy or sell trigger.
You mentioned, “One day I will write an article to explain my cost of equity capital methods in more depth.” I look forward to that. I was curious what you thought of Bloomberg’s WACC function.
After reading your link critiquing Bloomberg’s DDM, I would be curious to read you take on WACC and the EVA spread (economic value added, of course).
As always, thanks for the years of sharing your thoughts.
I agree with Jeff in that your analysis is excellent and thought provoking. I thought I’d share a couple of points. First, John Hussman has pointed out that the Fed Model has been a pretty good indicator as a sell signal for bonds rather than a buy signal for stocks.
I think the historical back testing raises a few issues. The 54 year period includes two secular bull markets and only one secular bear and the current end point is near all time highs. Using normalized profit margins, the average stock is at the very high end of the top historical decile for valuation. It also includes a 25 year period where the financial profits have grown to close to 50% of earnings and debt as a percentage of GDP has grown to 350% from around 100%. This explosion in financial profit growth due to leverage is very hard to replicate. This has largely been possible due to the dollars reserve currency status, but what are the chances that the dollar retains the same level of stature and debt to GDP goes to 600% over the next 25 years? Anything is possible but I find that outcome highly unlikely.
A truly global examination of history indicates that the US’s 20th century emergence and run as the largest global economic and political power is unlikely to continue. Many of the imbalances often sited are typical late-dynasty indicators. Whether it were the Spanish of the 17th century, the Danes of the 18th century or the British of the 19th century, all started their demise as we have – inflating currency with massive debt growth combined with imperial war.
Therefore, I would argue that the general underlying assumption that capitalist economies will grow at a 6-7% rate is faulty. This has likely been true historically during their maturity phase, but not in their decline. Growth rates have been much faster in their emerging phase – like the US in the late 1800’s, the Japanese in the 1960’s-1970’s and China today.
Of course, these are largely qualitative factors/risks, but then that is why value investing involves a margin of error. I doubt that Ben Graham would look at the average stock today as anything other than grossly overvalued.
Excellent analysis and write-up! Thanks for posting this.
You and one of the commenters mention John Hussman. As I’m sure you are aware, he has written several pieces in recent weeks critical of the Fed Model and pointing out that the role of interest rates in setting fair value for stocks is overstated. FWIW, I’m a regular reader of his weekly commentaries and have a large stake in the Hussman Strategic Growth fund for myself and client portfolios. I hope you don’t mind but I took the liberty of e-mailing him a link to this note. It’ll be interesting to see if he addresses your argument in a future weekly note.
As far as I can determine, your arguments in this note are completely rational and logical, and well supported by a lengthy historical quantitative analysis. This is the complete opposite of most of what I’ve read on the Fed Model advocate side. Most of what I’ve encountered basically amounts to hand-waving with no data support or extremely short time frames.
In any case, I am trying hard to reconcile your piece with Hussman’s recent notes. I am thinking that perhaps there is no contradiction. The focus of Hussman’s notes have been the absolute valuation on stocks and likely long-term (5-10 year) returns while you do point out the Fed Model is more about the relative valuation between stocks and bonds. In that sense, it seems like 95%+ of investment strategists are misusing and misapplying the Fed Model. They are using it to proclaim that stocks are screaming bargains while if you look at a metric like P/E and use 10-year average earnings stock valuations are about as high as they have ever been.
I guess the conclusion is to definitely avoid LT bonds, and keep any fixed income very short duration.
A bit off the subject, you mention other asset classes. I have a pretty hefty allocation to commodities, and I’m definitely in the commodity supercycle camp (Jim Rogers) and think there is alot of upside still there over the next 5-10 years. However, I am reevaluating my exposure because I am using a mutual fund that basically copies a passive index and uses the rolling futures strategy. Others and yourself have pointed out the distorted futures curve causing persistent losses on the roll. Do you have any solutions/ideas here?
Dear David,
Very, very useful post. Two questions for you, if I might:
1) “The first thing to remember is that the ?Fed Model? doesn?t tell you whether stocks are absolutely cheap, but whether they are cheap versus bonds.”
Is there such a thing as absolute cheapness. I’ve thought about it some, and I don’t understand how one goes about defining absolute cheapness, absent arbitrage. I’d appreciate your thoughts on this.
2) As with others, I am eagerly waiting to hear more about your “cost of equity capital methods” in more depth.
Finally, go to pimco.com, and check out Markowitz’s critique of CAPM. You’ll enjoy it, I think!
Is there such a thing as absolute cheapness. I?ve thought about it some, and I don?t understand how one goes about defining absolute cheapness,
AA,
I’m not David, but I’ll take a stab at this. My definition of “absolute cheapness” is a valuation level that is likely to deliver above-average long-term returns where long-term returns is at least 5 years and preferably 10 years, and above-average means at least greater than 10-11% which is the VERY long-term average for stocks. It seems almost obvious to me by definition that stocks were cheap in the past when they ended up delivering above-average long-term returns, and were expensive in the past when they ended up delivering below-average long-term returns. I’m not sure what other definition could make sense.
Based on the research I’ve read and studied from what I consider the sources who have done the best quantitative analysis on this subject (Hussman, Crestmont Research, James Montier) the single best indicator of the absolute cheapness of stocks is the P/E ratio or earnings yield IRRESPECTIVE of what interest rates happen to be. Low starting P/E ratios have been followed by high stock returns, and high starting P/E ratios have been followed by low stock returns. The following graph from Crestmont is instructive:
http://www.crestmontresearch.com/pdfs/Stock%2020%20Yr%20Returns.pdf
Now there are those who argue that essentially all data and historical experience prior to 1980 is irrelevant. I’m not sure how you can prove that point one way or the other, except that my opinion would be the more data the better.
Geoff Gannon has posted a great series of articles on valuation on seekingalpha (I think he has a blog as well). Bottom line, we have basically been in uncharted territory since 1996 and on. I see 2 outcomes:
1. We are in a new era of permanently higher valuations that will be maintained indefinitely and long-term returns from stocks will be below their long-term 10-11% average, or
2. At some point we will revert to more normal historical valuation levels. This will result in a substantial decline in stocks, but provide the starting point for higher returns going forward from that point on.
My focus at this point is trying to strike a balance between those 2. I think a middle ground of being cautiously bullish and focusing on stocks with attractive relative valuations makes sense. My sense is individuals like Hussman and Grantham are probably correct in their valuation concerns, but that this present market still has to go through the final parabolic blow-off stage.
Hello Mike C,
I would like to send you an email if you are ok with it – I can be contacted at james@teamfinancial.net
I too have a large investment in Hussman and I have some input for you on the commodities question.
I wanted to present another thought on the Fed Model coming from the perspective of trying to be open-minded about how to have portfolios positioned in terms of market exposure. Hopefully, this thought might generate some discussion.
Let’s put aside the question of whether the Fed Model is theoretically or empirically valid. The Fed Model certainly has some high intellectual horsepower critics in guys like Hussman and Asness. The more important issue might be how many in the investment world believe it is valid (and the AUM they control and buy/sell decisions they make) rather then whether it is actually a valid method for valuation of the broad stock market.
At the end of the day, the stock market is an auction market and as much as “valuation” might matter, especially in the long-term, it is ultimately supply and demand that determines the prices of securities. Ultimately, if the demand for stocks at current valuations is stronger then supply because the overwhelming majority of market participants believe in and are acting on the Fed Model, that may be the most important thing to realize about where stock prices are headed at least in the short-term. Stocks are worth whatever somebody else is willing to pay for them, and those people who believe in and act on the Fed Model are willing to pay current prices.
Based on what I read in the press, the blogs, and see on CNBC, it sure seems to me that the overwhelming majority of institutional money believes in using the Fed Model as a valuation tool (and I assume are actually acting on it), and presumably we are talking about hundreds of billions, if not over a trillion dollars of money under control.
Here is just a recent sampling of seeking alpha articles to support the idea that most are in fact using the Fed Model to make their decision to buy stocks:
http://usmarket.seekingalpha.com/article/41008
http://usmarket.seekingalpha.com/article/40945
http://usmarket.seekingalpha.com/article/31452
This is more then just an academic question to me. I currently have a roughly 30% cash allocation (after recently selling most of my REIT allocation), and a fairly high allocation to a defensive mutual fund (probably not hard to guess what it is). I’d be lying if I didn’t say I am concerned about potential underperformance if this market continues rising over the next 1-2 years, and I think it is a reasonable possibility we are entering a final blow-off parabolic stage to this bull market similar to 1998-early 2000. Ultimately, I think it will end very badly but in the meantime those cautious/bearish on the market may continue to look “stupid”.