I’ve long admired ECRI for their timely and accurate forecasts, and their willingness to stick by their models when things don’t seem to be immediately going their way.? I have also appreciated their lack of willingness to divulge their model elements; my thoughts were, “Hey, it’s probably a simple model that no one has ever thought of.? Would I reveal the model if I were in their shoes.? No.”
But I’m not in their shoes, and I know one of the ECRI pair, so I asked for some insight into the models, which he coldly refused.? Okay, fair enough, I’m not a paying subscriber, but we had had good conversations in the past, so I thought I might have some relational capital, but no.
Tonight, I bring you my kludge that should be close to the ECRI Weekly leading index.? I am not saying that I reverse-engineered it because in econometrics there may be many fits with equal probability that explain the dependent variable well.? But here we go.
Yesterday, I read a post at the Bonddad Blog that said it had all of the variables for ECRI’s Weekly Leading Index.? I decided to gather the data, or reasonable proxies of it, and I ended up using the following variables to estimate the ECRI WLI:
- M2 YOY % increase, SA
- AAA yields from Moody’s
- BAA yields from Moody’s
- S&P 500 price YOY % increase
- Initial Jobless Claims SA
- Real Estate Loans from all Commercial Banks, SA YOY % increase
- PPI for Industrial Commodities
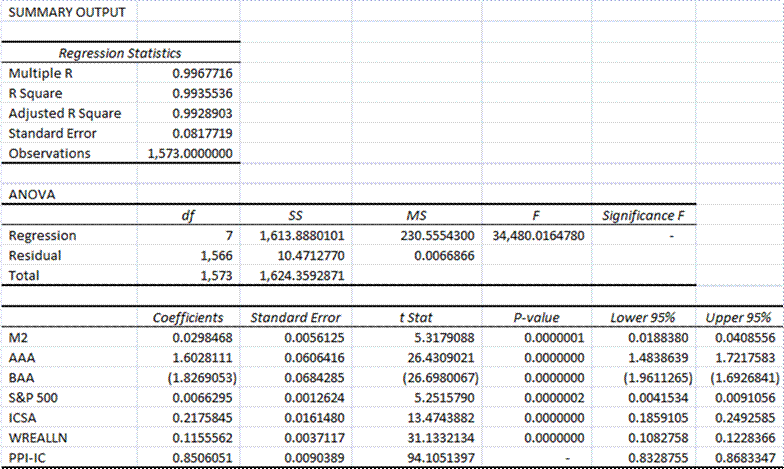
I realized the the independent variables had to go up and down because the WLI does as well.? I normalized the variables against their long run averages, which would have no impact on the fit if the regression, but would enable sorting out the size effects.? Anyway here are the results:
That’s a really high R-squared (normalized F), with highly significant t-coefficients.? What is more, the coefficients sum to materially one in this regression that constrains the intercept to zero.
So, we have a good guess at what drives the ECRI WLI: two items, Corporate interest rates and industrial commodity prices.? The other items are significant, but less material.?? BAA bond yields could be expressed as spreads against AAA yields, but the mathematical results would be the same.
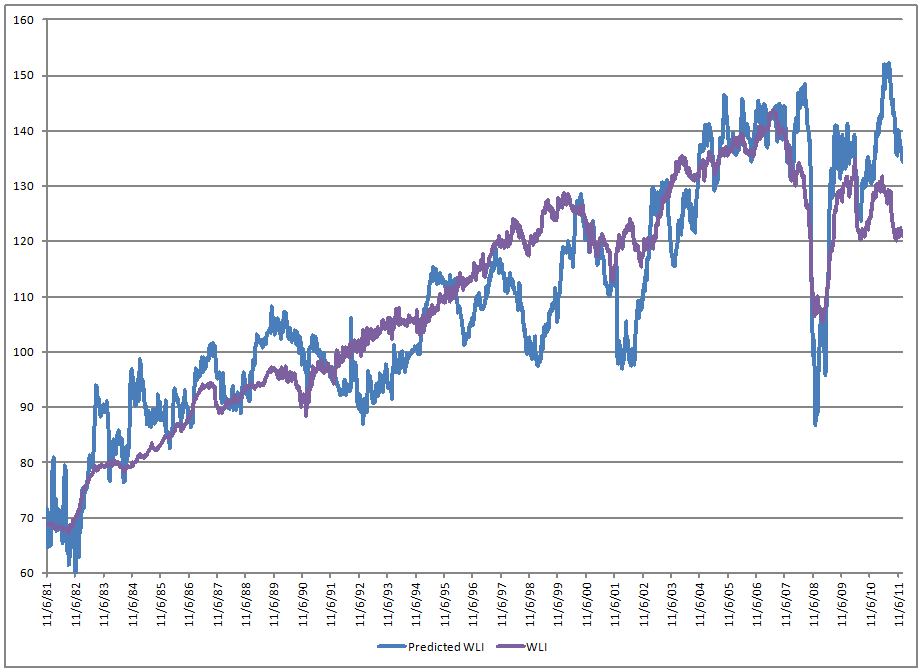
So how does my model fit against the ECRI WLI:
If anything, my estimated model is more sensitive than ECRI’s model.? I could have a new business here, except that I have given the model away for free.
Comments are welcome.

Hi David, Your model looks like a high beta version of the ECRI model. Could you add something to the formula to “de-risk” it so it moves less but maintains its correlation.
Sure, you would do a moving average of the results. ECRI does that already.
Hello David – I hope all is well with you and your family.
I get ECRI’s “light product” which is what we can afford at this point. I think the key to ECRI’s process is tat it is not a model in the traditional sense, but rather a process. I suggest anyone really interested in understanding what they do to read their book. The WLI is just one part of their process and the level off any of their leading indicators need to display what they call the three p’s- persistence, pronounced and pervasive.
Personally I think many miss the forest. For the trees in trying to focus on the WLI when the competitive advantage they have is rooted in the process – at leat IMO.
Apologize for poor grammar – fat fingers on the iPad!
If you run a regression of the magenta line on variables that have similar trends, you will get a spuriously high R2. I think you should try to explain the weekly changes in the magenta series instead. (I may have misunderstood you regression, in which case please show the actual data series in the regression so I’ll understand it better.)
I e-mailed you a spreadsheet with the JOC-ECRI index data. If you didn’t get it let me know. I looked for the Dun and Bradstreet insolvency Index but so far with no success.