I appreciate Eddy Elfenbein.? He comes up with ideas that make me say, “Huh. Interesting.? Let’s test that.”? His recent article, World?s Simplest Stock Valuation Measure, put forth the idea that:
Growth Rate/2 + 8 = PE Ratio
Cool, reminds me of my 1993 formula for value investing:
Price per share < Tangible Book per share + 5 * EPS
Eddy’s idea is that you can buy a company that isn’t growing or shrinking earnings at a PE of 8, or alternatively, a E/P (earnings yield) of 12.5%.? In a weird environment like this, it means an earnings yield that is more than 9% over the long bond is a good purchase.? I like that idea, it offers a good reward for taking risk.
But as the growth rate rises, you can expand the PE multiple by half of the anticipated growth rate.? So, a company anticipated to grow at a 10% rate would warrant a PE multiple of 13, a 20% rate 18, etc.? I like his formula, because it is conservative.? It seeks growth at a reasonable price.? It will not overpay for high growth rates.
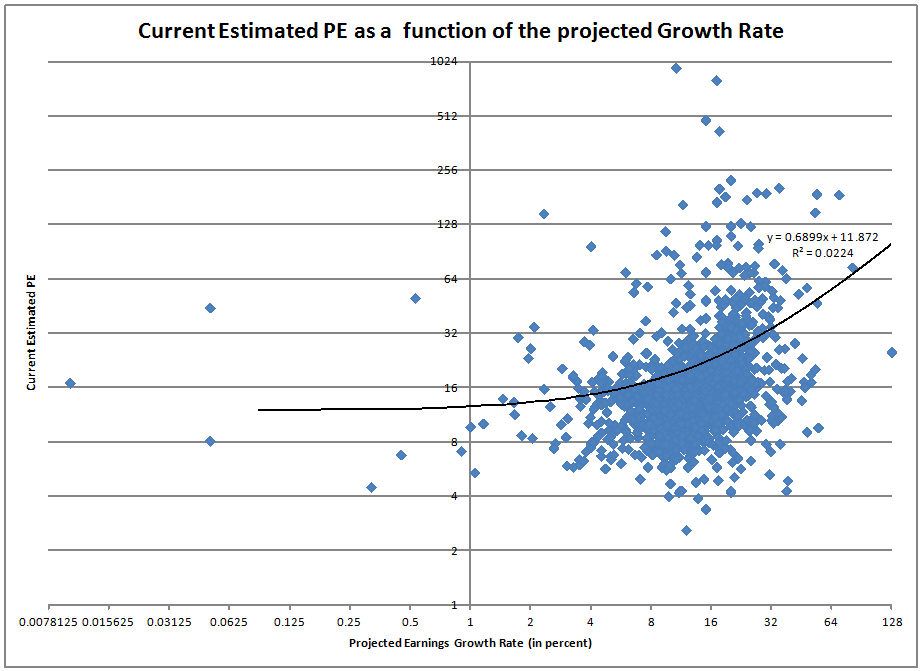
But now let’s test this statistically to see what validity it presently has.? I ran a regression on Current year expected PEs versus expected 3-5 year growth rates.? I excluded all companies with fewer than two analysts putting forth growth estimates.? Here were the results:
| SUMMARY ?OUTPUT | ||||||||
|
Regression Statistics |
||||||||
| Multiple R |
0.15 |
|||||||
| R Square |
0.0224 |
|||||||
| Adjusted R Square |
0.0218 |
|||||||
| Standard Error |
39.70 |
|||||||
| Observations |
1,589 |
|||||||
| ANOVA | ||||||||
|
? |
Df |
SS |
MS |
F |
Significance F |
|||
| Regression |
1 |
57,333 |
57,332.91 |
36.38 |
0.000000002 |
|||
| Residual |
1,587 |
2,500,838 |
1,575.83 |
|||||
| Total |
1,588 |
2,558,170 |
||||||
|
? |
Standard Error |
t Stat |
P-value |
Lower 95% |
Upper 95% |
Eddy |
T-test |
|
| Intercept |
11.87 |
1.88 |
6.33 |
0.0000000003 |
8.19 |
15.55 |
8.00 |
2.06 |
| eps_eg5 |
0.69 |
0.11 |
6.03 |
0.0000000020 |
0.47 |
0.91 |
0.50 |
1.66 |
?
Significant results statistically, but what a low R-squared.? Just shows us all how complex the market really is.? Look at this graph to see it as it is:
There really doesn?t seem to be much of a relationship.? But Eddy?s formula is conservative versus the estimates.? His formula invests in no-growth? companies ?at an earnings yield of 12.5%, the market does so at an earnings yield of 8.4%.? His formula increases the PE multiple at a 50% rate as earnings increases, but the market does so at a 69% rate.
Good for Eddy, and any that follow him.? His method builds in a margin of safety, which is a key to all good investing.
Before I close I would like to offer the 20 most mispriced companies, both positively and negatively.? Just be aware that the markets are complex, and this valuation method is simple, and most likely wrong? but it can provide a jumping-off point for due diligence.
Potential Buys
| company | ticker | eps_eg5 | PE |
| Seagate Technology PLC | STX |
37.94 |
4.3 |
| US Airways Group, Inc. | LCC |
38.5 |
4.9 |
| China Xiniya Fashion Ltd (ADR) | XNY |
12 |
2.6 |
| Exide Technologies | XIDE |
15 |
3.4 |
| HollyFrontier Corp | HFC |
31.19 |
5.3 |
| First Solar, Inc. | FSLR |
20 |
4.2 |
| Xerium Technologies, Inc. | XRM |
20 |
4.3 |
| YPF SA? (ADR) | YPF |
13.69 |
3.9 |
| Newmont Mining Corporation | NEM |
54.68 |
9.6 |
| Western Digital Corp. | WDC |
20.84 |
5.1 |
| Gulfport Energy Corporation | GPOR |
48 |
9.1 |
| Delta Air Lines, Inc. | DAL |
17.25 |
4.9 |
| KKR & Co. L.P. | KKR |
22.43 |
5.7 |
| Dana Holding Corporation | DAN |
31.56 |
7.1 |
| Perfect World Co., Ltd. (ADR) | PWRD |
9.78 |
4 |
| Marathon Petroleum Corp | MPC |
25.16 |
6.3 |
| Stoneridge, Inc. | SRI |
35.2 |
7.8 |
| GT Advanced Technologies Inc | GTAT |
11 |
4.2 |
| Telecom Argentina S.A. (ADR) | TEO |
11.3 |
4.3 |
| SUPERVALU INC. | SVU |
11.1 |
4.3 |
Potential Sells
| Company | Ticker |
eps_eg5 |
PE |
| Rubicon Technology, Inc. | RBCN |
15 |
125.6 |
| NetSuite Inc. | N |
34.79 |
204.1 |
| Amazon.com, Inc. | AMZN |
30.02 |
190.6 |
| Clear Channel Outdoor Holdings | CCO |
24.04 |
175.5 |
| Servicesource International In | SREV |
27 |
192.1 |
| Wright Medical Group, Inc. | WMGI |
9.43 |
117.1 |
| Lamar Advertising Co | LAMR |
4 |
96.8 |
| Cogent Communications Group, I | CCOI |
17 |
170.5 |
| Shutterfly, Inc. | SFLY |
18.75 |
182.6 |
| Lattice Semiconductor | LSCC |
11.5 |
165.3 |
| Conceptus, Inc. | CPTS |
17.5 |
201.6 |
| Cepheid | CPHD |
20 |
225 |
| Black Diamond Inc | BDE |
2.33 |
146.9 |
| Quidel Corporation | QDEL |
17.5 |
421.5 |
| WebMD Health Corp. | WBMD |
15 |
485.1 |
| SL Green Realty Corp | SLG |
-3.09 |
230.2 |
| Diana Shipping Inc. | DSX |
-16.62 |
11.4 |
| Netflix, Inc. | NFLX |
16.96 |
803.8 |
| Citi Trends, Inc. | CTRN |
10.67 |
942.7 |
| Weatherford International Ltd | WFT |
-30.72 |
11.4 |
That’s all for now.

This is similar to and a somewhat more conservative version of Benjamin Graham’s formula:
PE = 8.5 + 2 x Growth Rate
FWIW, you can actually derive this as a simplification of standard DCF model (assuming constant perpetual growth).
Just start with:
PE = 1 / (R – G)
(where R is the discount rate and G is the perpetual growth rate).
Take the Taylor expansion (treating G as the variable and R as a constant) and truncate the nonlinear terms and you get:
PE = 1/R + 1/R^2 x G
Notice if R = .125 then the equation reduces to something pretty close to Eddy’s:
PE = 8 + .64 x G
(Note: G is multiplied by 100 and expressed in percentage terms)
It should be noted that some of the nonlinear terms that were truncated are not negligible for a decent sized growth rate so that needs to be taken into consideration (that and the fact that nothing grows perpetually at constant rates.)
This is close to a simple PEG. I can put directly in the Yahoo stock screen.
I will often add (.25 <= PEG <= .75) and (3 <= PE <= 15) to my search rqmts.