The relationship of the VIX to the S&P 500 is an interesting one, one that I have studied for the past nine years. Over that time, I have used the relationships to:
- Design investment strategies for insurance companies selling Equity Indexed Annuities.
- Estimate the betas of common stocks. (Not that I believe in MPT?)
- Trade corporate bonds.
- Gauge the overall risk cycle, in concert with other indicators.
If there is interest on the part of readers, I can go into the details of any of the above. Perhaps that could be the basis for future articles in this series. Today?s article is on the following relationships:
- The relationship of percentage changes in the old VIX to percentage changes in the S&P 500.
- The relationship of the old VIX to the new VIX.
- How quickly does the VIX mean revert, and
- The relationship of the VIX to price levels of the S&P 500.
- Maybe there will even be some hints at profitable trading rules. 🙂
The relationship of percentage changes in the old VIX to percentage changes in the S&P 500
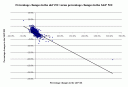
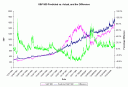
I have a rule of thumb that I calculated a long time ago that the percentage change in the old VIX (and the new VIX, almost) is usually about ten times the percentage change in the S&P 500, and with the opposite sign. Well, I went and re-estimated the relationships. What do they look like?
The best fit line almost goes through the origin, and the slope is ?0.0993. Inverting that, the value for my rule of thumb is 10.07. (Hey, that?s pretty close!) The best fit line explains about 50% of the variation in changes in the S&P 500.
I used the Old VIX because the data goes all the way back to the beginning of 1986, versus the new VIX, which starts at the beginning of 1990.
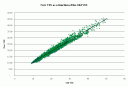
The relationship of the old VIX to the new VIX
I think differences in the two measures can be overstated. The two measures are 98.6% correlated. This equation describes the relationship:
New VIX = 2.04 + (Old VIX * 0.86)
The relationship is tighter when the VIXs are low, and gets a touch looser when the VIXs gets higher (no surprise, many relationships get strained in volatile times. That also implies that percentage changes in the new VIX should be about 86% of the changes in the old VIX, so my rule of thumb applied to the new VIX would be, ?The percentage change in the new VIX is usually about 8.6 times the percentage change in the S&P 500, and with the opposite sign.? Still close to 10. I can live with that.
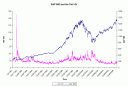
How quickly does the VIX mean revert?
Back in 1998, when I was developing my first generation old VIX / S&P 500 models, I came up with a statistic that said that the VIX mean-reverted to a level of 16, and it would tend to return at the rate of 20%/month, while being jolted by random disturbances pushing it to and away from the mean. The jolts are more powerful in the short run, but the mean-reversion is like gravity, inexorably pulling.
I have nine years more data now. Much of that time was a higher VIX era, so it is no surprise that the mean reversion target is 18.94. What is more interesting is that the reversion happens a little faster, at a rate of 28.2%/month, which means absent other disturbances, it closes half of the gap to the mean reversion target over 44 days. (Hey, pretty close to 50 days? could that be significant?)
This helps to show that snapback rallies after crises are so reliable in their appearance. Given the strength of the mean reversion effect in volatility, for the VIX to stay elevated for a long period of time requires a series of crises akin to what we had in 1998-2002.
I experienced the pain of that firsthand managing mortgage and then corporate bonds. Bond yield spreads are very highly correlated with the implied volatilities of stocks, and the yield spreads on bond indexes are highly correlated with the implied volatility on broad market equity indexes, like the VIX.
(Note for wonks: I estimated the mean reversion level (which is very close to the historic mean, no surprise) by regressing the one-day lagged Old VIX on the Old VIX itself. If you want how the math works on that, I can provide it, but it will make most readers go ?huh??)
The relationship of the VIX to price levels of the S&P 500
Finally, the most controversial bit. The S&P 500 tends to be lower than trend when the VIX is high, and higher than trend when the VIX is low. In equation form, it would look like this. (Sn is the S&P 500 at time n, and the same for V, the Old VIX. The V with a bar over it is the mean reversion target for the VIX.
In other words, the S&P tends to rise at a constant rate r, over time n, unless the VIX is above or below its long run average. Now, this is an oversimplification. I am using a very simple function form to allow me to come up with a result for now. There is probably some better functional form our there based off of Black-Sholes, or something like that, that wil do a better job. This is what I have for now.
Taking logs and simplifying, I get:
I know the S&P 500 and the old VIX over time, so I can estimate the parameters a, r, and e. The regression explains 88% of the variation in the S&P 500. a works out to be 4.94, which implies an S0 of 263.42, which is not far off from the actual starting value of 242.17. The rate of growth for the S&P 500, r, is 9.30% which is consistent with the actual result of 9.45% (not counting dividends, and running from 1987 to the present). Finally, e, the shape parameter on the old VIX is 21.5%. What this means is when the old VIX is double its mean-reversion target, the S&P 500 should be 16% above trend, and when the old VIX is half its mean-reversion target, the S&P 500 should be 14% below trend.
Wait, isn?t that backwards? How can a high VIX be associated a high price for the S&P 500, and vice versa for a low VIX? (I blinked when I first saw this, but the coefficients are statistically significant at a very high level.) This is my explanation: when the VIX is high, the equation anticipates mean-reversion, and so gives a value that reflects what the S&P will be worth once volatility mean reverts. Vice-versa for when the VIX is low.
What does that imply for today? Putting the old VIX closing value of 25.18 into the equation would predict an S&P 500 price of 1898.90, a little more than 30% above the current quote. Time to buy!
Limitations
Well, not so fast. This is a deliberately simplified model compared to the realities of the market. Does the S&P 500 go up 9.3% annually? No, but over a long period, it seems to. Do I have the right functional form for the effect of the VIX? No, but this equation will be right to a first approximation. What about interest rates? Couldn?t they be included as a valuation parameter? Sure, maybe in the next round. They certainly helped in the ?Fed Model.?
Don?t I have lookback bias here? If I were back in early 1987, would I think that the mean reversion target for the VIX should be 18.94? Maybe back then, but one would scratch his head in 1994, 2002, and 2006. The data fits very well inside the sample, but how well it will work in the future is always open to question. Every economic era is special, and blindly applying old parameters when the game might be changing is dangerous.
Possible trading rules
All that said, here are a number of trading rules that can be concocted from this study, and many work in hindsight. They boil down to buy when the VIX is high (panic), and sell when it is low (complacency). In future posts, I can work through a few of them, subject to the warning that data-mining can be hazardous to your financial health. (I have tried to pass through the data as few times as possible, but I have doubts?) I have found that being picky can generate big gains, but with few signals over long time periods (wait, isn?t that just the rise in the market?), and shorter-term systems generate many signals, but over short time spans, for small gains.
As an example of a system, you can look at Babak?s method using distance of the VIX from its 50-day moving average. 50 days? Close to the half-life mean reversion time. Looks like it can generate some good trades. Anyway, more later; hope you enjoyed this article.

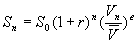
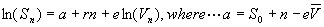
Being in a firm that trades VIX regularly and builds quant models in-house, I would love to read more studies on what you’ve discovered in how to trade the VIX or build models using the VIX as a signal to picking sectors to be in.
Great blog, by the way. I’m a daily reader!
I just discovered that clicking on your pictures results in an error. They won’t enlarge as the link won’t engage. Any way you can fix this?
Excellent work, David. Lots of things to ponder in here, though I can’t seem to get the graphics to load for me.
Ironically, I posted something similar to some of your work yesterday: http://vixandmore.blogspot.com/2007/07/spxvix-ratio-mean-reversion-magnet-and.html
Needless to say, I am eagerly anticipating the next installment.
Cheers,
-Bill
Note for wonks: I estimated the mean reversion level (which is very close to the historic mean, no surprise) by regressing the one-day lagged Old VIX on the Old VIX itself. If you want how the math works on that, I can provide it, but it will make most readers go ?huh??
I’d like to see this math, please, in an effort to replicate it on my end.
Hi,
Great great great article! I’m a student writing a paper on just this topic, such a coincidence! My friend told me about you blog. Thanks!
However I only though about it (VIX, P/E, S&P500, …) about two weeks ago and the (luckily short) paper is due the 20th. It’s for statistics. I’m going to contact you (who? author?) via email (maybe we could help each other out, email graphs and the mathimatical stuff that most people don’t get – sorry guys)!
Oh, and sorry if there are any spelling mistakes and stuff. I’m excited.
Greetings from Belgium!
Fascinating stuff. I think your regression in the first graph (VIX vs S&P 500) is being heavily skewed by your outlier at +300%. I would remove it and see how much it changes, because I think this will make a big difference.
Also, technically such a direct linear correlation is impossible. Since the S&P 500 has increased consistently over time, the VIX would need to decrease consistently over time. Which is why your subsequent model is much better in terms of fit.
Finally, I’m not getting your derivation of a. When I do it I get a bunch of lns in there.
Anyway, thanks for putting this out there.
Very interesting article. This article looks at the relationship between the VIX and the S&P like I have never seen before. This is almost a contrarian article of a contrarian thought, pretty neat.