I’ve estimated a number of mean-reverting models in my time. I had one of the best dynamic full yield curve models around in the mid-90s. The investment department at Provident Mutual said it was the first model that was not artificially constrained that behaved like the yield curve that they knew.
In yesterday’s article, I mentioned that I could give math behind estimating mean-reversion of volatility. In order to do the regression to estimate mean-reversion, we use a lognormal process, because volatility can’t be negative.
Taking the logs of both sides:
Alpha is the drift term, that will help us calculate the mean reversion level, beta is the daily mean reversion speed, and epsilon is a standard normal disturbance term. Assume that there are no more random shocks, so that the volatility returns to its equilibrium level, which implies:
Substituting into the log-transformed equation, we get:

where V-bar is the mean reversion level for volatility. From there, the solution is straightforward:
From my regression, alpha equals 0.046000, and beta is 0.98436. That implies a mean reversion target of 18.937, and that volatility moves 1.564% toward the mean reversion target. One last note: the standard deviation of the error term was 6.3383%, which helps show that in the short run, the volatility of implied volatility is a larger effect than mean-reversion. But in the long-run, mean-reversion is more powerful, because with the law of large numbers, the average of all the disturbances gets closer to zero.

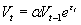
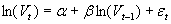
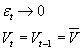
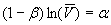
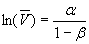
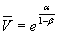
Hi, I am currently developing a mean reversion model for implied volatility but i need some sample data or webiste that provide the mean reversion rate with the option pricing to validate my work.
do you have any ide where i can find it ?
Thanks
Can you reject the hypothesis of a random walk, i.e. alpha = 0, beta = 1.
Yes, it is rejected. The t-statistics are 6.32 and 6.37 respectively. The prob-values are roughly 3 in a billion.