Uh, this is an off-topic piece. One of the benefits of working from home is that I can listen to my wife teaching our children, and every now and then, I drop in and explain some aspect of the topic further. Out of the corner of my ear, I heard my wife Ruth explaining Greatest Common Factors and Least Common Multiples to our fifth child, Jonathan.

When I was a kid, I was kind of a prodigy with math (I am not so now), and when we went through it in school, I remember tutoring my classmates on the two topics. I always thought the two concepts were related, but I never understood how, until it struck me last week.

Consider the numbers 60 and 144. What are their Greatest Common Factors and Least Common Multiples? To start, let’s factor the two numbers:

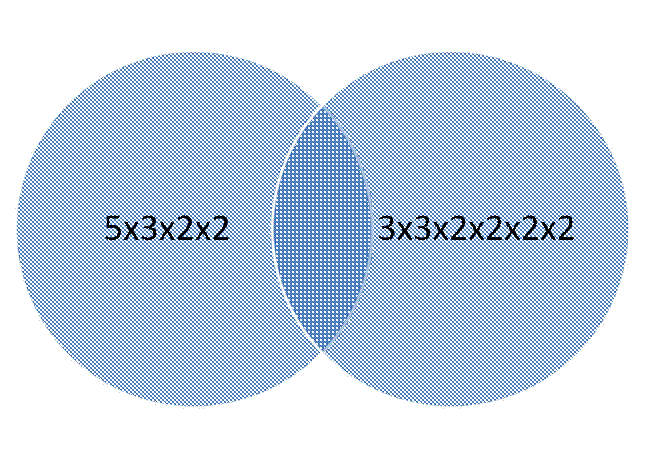
Then, let’s place the common factors in the intersection set.

The greatest common factor is the product in the intersection set, in this case, 3×2x2 = 12. The product of the union set (just multiply across) is the least common multiple — 5×3x2×2x3×2x2 = 720.

When I realized this, I drew it out for Ruth and Jonathan, and told them “Look at the ravings of a madman.” But later that evening, Ruth came to me and thanked me for it, because it worked with Jon, and clarified it to her.

As a mathematician, I am nothing great, but my intuition has been a great help to me at many points. This was one of them.

Update Saturday Afternoon

As F comments, “Which has the consequence that LCM*GCM = number1*number2.”

I should have written that myself, but didn’t.  Thanks for pointing that out.  It is an application of the rule that:

set A + set B = union of A&B + intersection of A&B

This entry was posted on Saturday, May 3rd, 2008 at 1:59 am and is filed under Home Schooling. You can follow any responses to this entry through the RSS 2.0 feed. You can leave a response, or trackback from your own site.