=======================

If you are famous and dead, many people will attribute clever sayings to you that you never said. ?As Yogi Berra said:

I really didn?t say everything I said.

Except that Yogi did say that.? Now, if Einstein didn’t do enough for us, he supposedly made many statements praising compound interest, but the articles I have seen haven’t been able to trace it back to an original source. ?Personally, I think compound interest is overrated, because business processes can’t forever compound wealth at a steady rate.

But some also have tried to credit Einstein with the Rule of 72. ?You know, the rule that says the time it takes to double your money in years is equal to 72 divded by the annual compound interest rate expressed as as an integer. ?E.g., at 8% your money doubles in 9 years. ?At 9% you money doubles in 8 years.

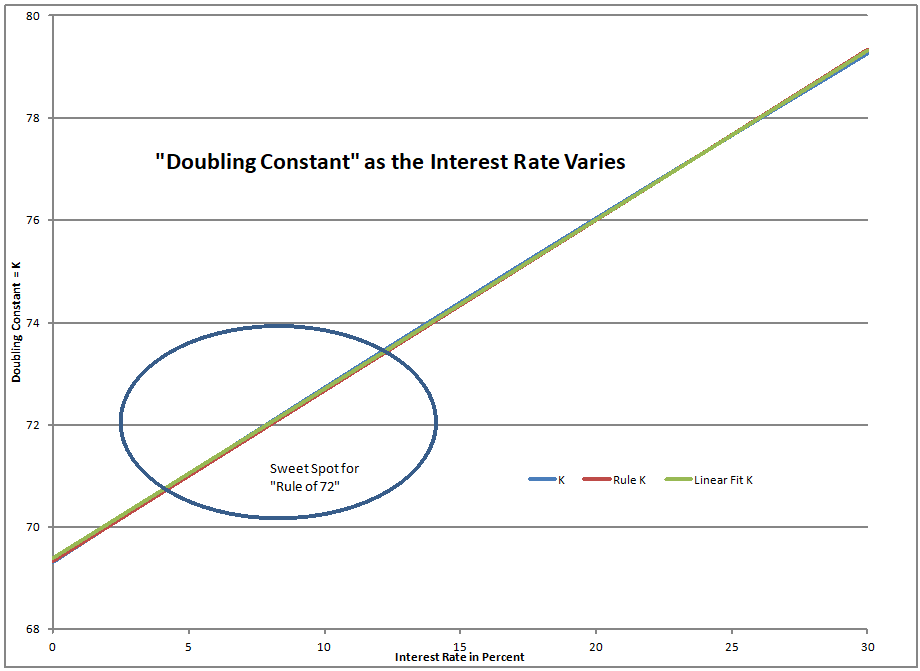
Pretty nice, and easy to remember. ?It is an approximation though. ?If Einstein ever did look at the rule of 72, he would have noticed that the approximation is pretty good between 3% and 13%. ?Outside that it gets further away.

One advantage of the rule of 72 is that it is simple. ?The second one is that 72 = 3 x 3 x 2 x 2 x 2. ?That makes it divide more intuitively by many integral interest rates, e.g., 3, 4, 6, 8, 9, 12 — allowing for some intuitive interpolation to aid it.

There is a more complex version of the doubling rule though:

The doubling constant starts (in the limit) at 100 times the natural logarithm of 2 [69.3147], and increases almost linearly from there. ?If you estimate a “best linear fit” line on the observations where the interest rate is between 0 and 30, the R-squared will be over 99.98%. ?The equation would be:

K = 69.3856 + 0.3313 * interest rate ?[Linear Fit K]

To make it a little more memorable rule, it can be turned into:

K = 70 + (interest rate – 2)/3 ?[Rule K]

Thus at 2% the doubling constant would be 70 — money doubles in 35 years. ?At 5%, 71, money doubles in 14.2 years. ?8% is the rule of 72 — nine years to double. ?At 11%, 73, 6.6 years to double. ?At 14%, 74, 5.3 years to double. 17%, 75, 4.4 years to double. 20%, 76, 3.8 years to double. ?I did those in my head.

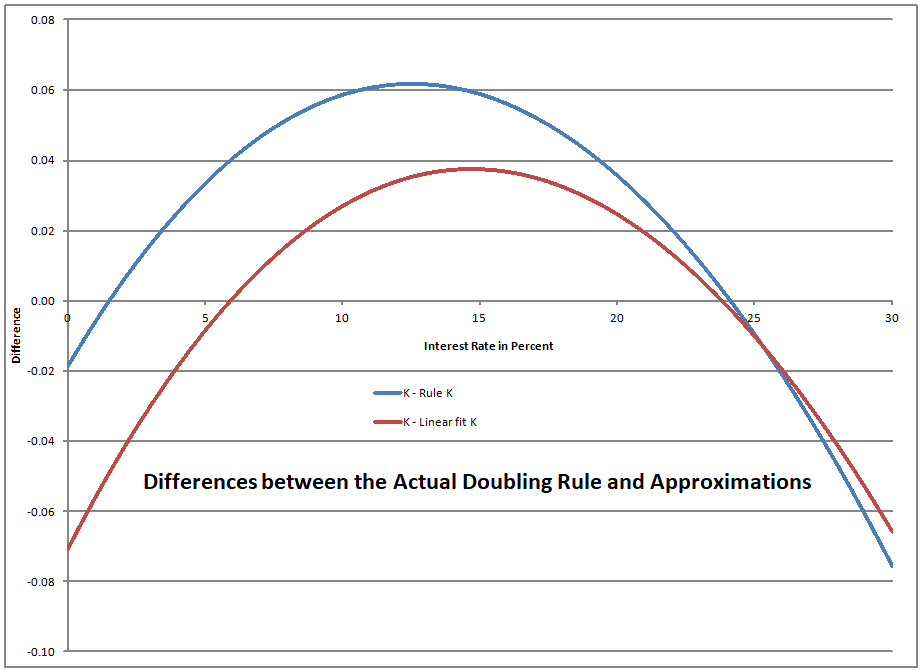
As you can see from the graph above, the actual doubling constant and its two approximations lie on top of each other. ?Not that I hope we see ultrahigh interest rates, but Rule K does quite well over a long span of rates. ?Here’s how small the deviations are:

Now, almost no one will use “Rule K” because the two advantages of the Rule of 72 are huge, and if interest rates get really high, someone could create an easy smartphone app to calculate the doubling period. (and constant if they wanted)

This is interesting for me, because I ran across what I call the “Rule of K” earlier in my career, and I was able to reproduce it on my own after reading the WSJ article that I cited above. ?Who knows, maybe Einstein took the doubling rule and did a first order Taylor expansion around 2% — that would have produced something very close to the “Rule of K” back when regressions were hard to do.

That’s all, and if you made it this far, thanks for bearing with me.