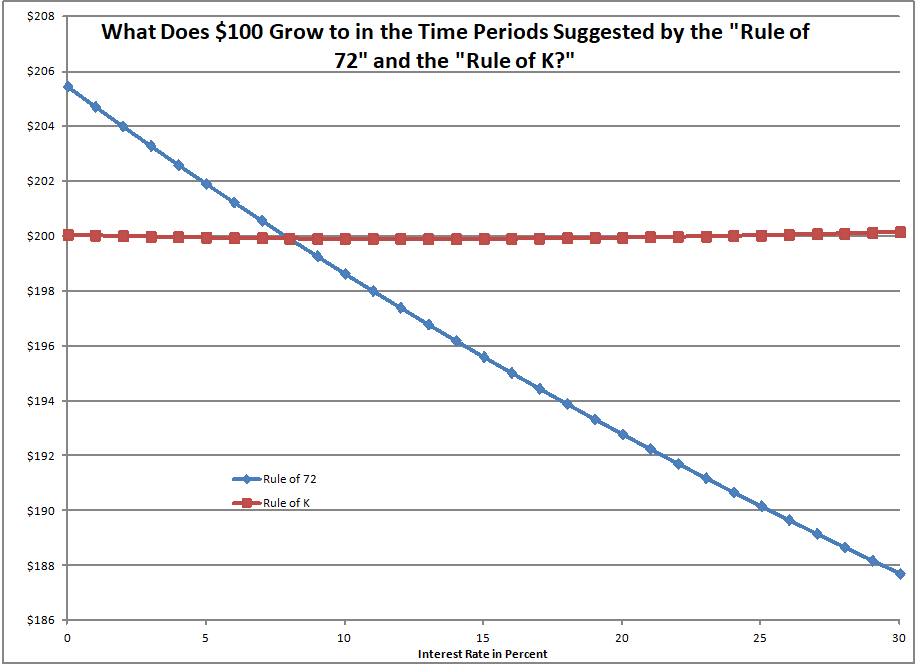
This is a small update of my last piece. ?I wish that I had put this graph in that piece, because it completes it.

Over the interest rate range of 0% to 30%, the average absolute deviations from perfect doubling using the Rule of 72 was 2.794%. ?Given the simplicity of the Rule of 72, that is wonderful.

But the “Rule of K” is virtually exact. ?The average absolute deviations from perfect doubling using the Rule of K was 0.036%.

Is this great? ?Well, with modern computers, exactitude is easy to come by. ?But if you are in a pinch to figure out the time to double, and all you have is a pencil and paper, the rule of K can do it with addition, subtraction and division. ?No fancy powers or logarithms. ?A four-function calculator will handle it, which, if you are using a rate that does divide into 72 easily, you will still need for the calculation.

At 8% the two are equal. ?Near 8%, the Rule of 72 is pretty good. ?The Rule of K gives an almost exact answer at the cost of a little complexity. ?Your choice depends on whether you need exactness or simplicity when all you have to work with is a four function calculator.

The Rule of K: If R is the interest rate multiplied by 100, money doubles in K/R years, where K = 70 + (R – 2)/3